Pembuktian Teorema 4 Geometri Insidensi

Teorema 4 dari Geometri Insidensi mengatakan, bahwa jika dua garis yang berbeda berpotongan, maka kedua garis itu termuat dalam tepat satu bidang. Pada kesempatan ini kita akan membuktikan Teorema keempat dari Geometri Insidensi ini.

Pertama, kita menulis apa yang diketahui dari teorema diatas,

Diketahui :

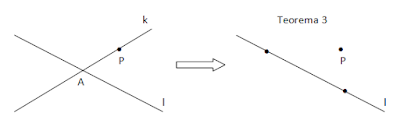
Sebelumnya kita bisa ilustrasikan teorema seperti gambar dibawah ini,

1. Garis k dan l dengan k ≠ l dan berpotongan di A

Akan Dibuktikan :

k dan l termuat tepat satu bidang

Bukti :

k dan l dengan k ≠ l berpotongan di A   ...diket

Pilih satu titik sembarang sebutlah titik B pada k dengan B ≠ A   ...Aks.1

Pilih satu titik sembarang sebutlah titik C pada l dengan C ≠ A   ...Aks.1

Titik B yang dipilih sembarang pada k dengan B ≠ A tidak mungkin terletak pada l. Demikian juga titik C yang dipilih sembarang pada l dengan C ≠ A tidak mungkin terletak pada k.   ...Teo.1 dan Aks.2

Titik A, B, C berbeda dan tidak segaris

Titik A, B, dan C termuat tepat satu bidang   ...Aks.4

Karena B dan C dipilih sembarang, maka garis k dan l termuat tepat satu bidang. Terbukti.

Baca Juga : Daftar Pembuktian Teorema Geometri Insidensi lainnya disini

Variasi Pembuktian/ Versi Lain :

Sobat juga bisa membuktikan Teorema 4 dengan cara lain, misalkan dengan memakai Teorema 3.

Bukti :

Pilih dua titik sembarang di k atau l, misal kita pilih k.

Pilih satu titik di k (sebarang), misal titik P, dimana tidak pada garis l dan tidak sama pada titik potong, P ≠ A.

Jadi terdapat sebuah garis l dan sebuah titik P, dimana P ∉ l. Sehingga berdasarkan Teo.3 termuat tepat satu bidang. Terbukti.

Itulah pembuktian untuk teorema 4 dari Geometri Insidensi, kita akan melanjutkan pembuktian Teorema 5 pada Geometri Insidensi pada artikel berikutnya.